In questo articolo impariamo a ordinare un array in c.
A cosa serve ordinare un array?
Immaginiamo per un attimo di prendere il libro di storia, aprirlo e vedere sulla prima pagina il numero 27. Perplessi giriamo pagina e ci troviamo davanti un bel 51, poi un 12, un 99 e così via. Cosa facciamo se il professore ci chiede di andare alla pagina 80? Ci mettiamo la mani tra i capelli!. Forse, qualche ora dopo, l’avremo trovata. Ordinare un array ci permette di trovare le informazioni al suo interno in maniera più veloce.
Algoritmi di ordinamento
Per ordinare una sequenza di elementi possiamo utilizzare diversi algoritmi, ognuno di essi ha i propri punti di forza e di debolezza, vediamoli nel dettaglio.
Selection Sort
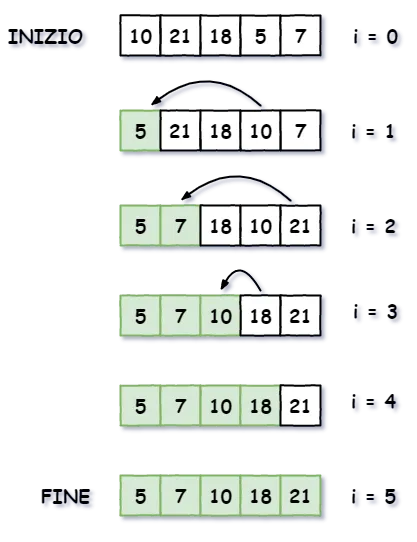
Il selection sort è un algoritmo di ordinamento molto semplice, partendo dall’inizio dell’array (con i = 0) :
- Scorre l’array e trova l’elemento più piccolo
- Scambia l’elemento più piccolo con l’elemento in posizione i
- Incrementa i
- Ripeti finché i è minore della lunghezza dell’array.
Pro
- Algoritmo molto semplice da implementare.
- Fa pochi spostamenti (al massimo tanti quanto la lunghezza dell’array), quindi è ottimo per ordinare elementi di grandi dimensioni.
Contro
- Inefficiente quando il numero degli elementi diventa importante.
- La velocità non cambia a seconda di quanto è ordinato l’array. (A parità di lunghezza, un array con un solo elemento disordinato impiegherà praticamente lo stesso tempo di un array completamente disordinato).
void selection_sort(int arr[], int lunghezza) {
int i,j;
int numero_minore;
for (i = 0; i < lunghezza-1; i++){
numero_minore = i;
for (j = i + 1; j < lunghezza; j++){
if (arr[j] < arr[numero_minore]) {
numero_minore = j;
}
}
int tmp = arr[i];
arr[i] = arr[numero_minore];
arr[numero_minore] = tmp;
}
}
Bubble Sort
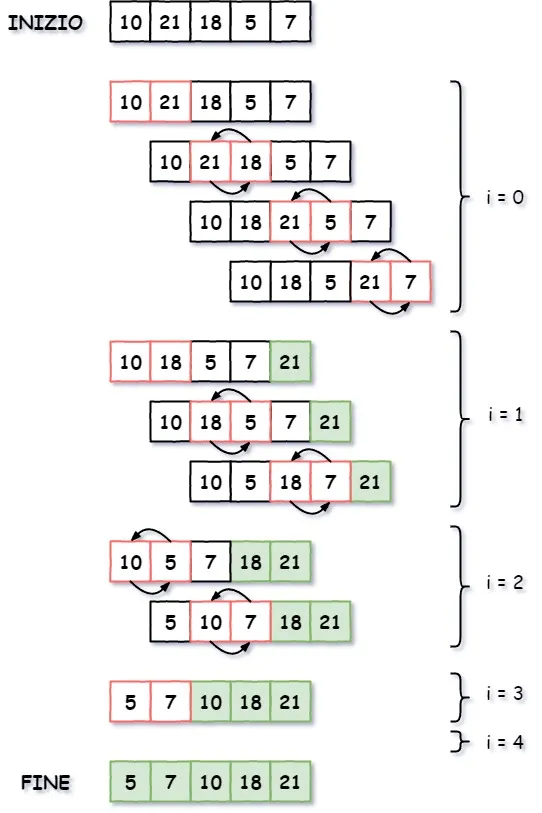
Il bubble sort è un algoritmo di ordinamento anch’esso molto semplice. Deve il suo nome al modo in cui ordina gli elementi, spostandoli “verso l’alto” come le bollicine in una sprite.
Partendo dall’inizio dell’array (con i = lunghezza dell’array) :
- Prende i primi due elementi e se il primo è maggiore del secondo li scambia
- Prosegue scambiando gli elementi fino alla fine dell’array
- Decrementa i
- Ripete finchè i maggiore di 1.
Pro
- Algoritmo molto semplice da implementare.
Contro
- Molto inefficiente, la sua velocità diminuisce drasticamente all’aumentare della lunghezza dell’array. Complessità (O n^2)
void bubble_sort(int arr[], int lunghezza) {
int i, j;
for (i = 0; i < lunghezza - 1; i++){
for (j = 0; j < lunghezza - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
Merge Sort
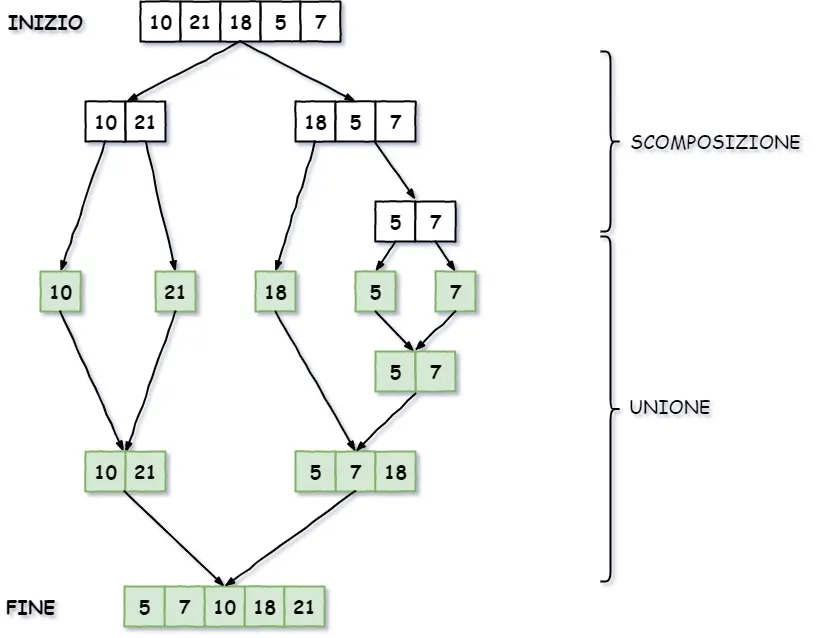
Il merge sort è un algoritmo un po’ più complicato. L’array viene scomposto nei suoi elementi per poi essere riunito in maniera ordinata. Per fare questo ci si avvale della ricorsione.
Partendo dall’inizio dell’array (con sx = 0 e dx = lunghezza dell’array) :
- Trova la metà dell’array compreso tra sx e dx
- Richiama il punto 1 per la prima metà (sx = 0 dx = metà)
- Richiama il punto 1 per la seconda metà (sx = metà + 1 dx = lunghezza dell’array)
- Unisce le due metà
Pro
- Prestazioni elevate, complessità (O n log n)
Contro
- Più complicato da implementare rispetto ai precedenti.
void unisci(int arr[], int sx, int m, int dx)
{
int i, j, k;
int lunghezza1 = m - sx + 1;
int lunghezza2 = dx - m;
int SX[lunghezza1];
int DX[lunghezza2];
for (i = 0; i < lunghezza1; i++){
SX[i] = arr[sx + i];
}
for (j = 0; j < lunghezza2; j++){
DX[j] = arr[m + 1 + j];
}
i = 0;
j = 0;
k = sx;
while (i < lunghezza1 && j < lunghezza2)
{
if (SX[i] <= DX[j])
{
arr[k] = SX[i];
i++;
}
else
{
arr[k] = DX[j];
j++;
}
k++;
}
while (i < lunghezza1)
{
arr[k] = SX[i];
i++;
k++;
}
while (j < lunghezza2)
{
arr[k] = DX[j];
j++;
k++;
}
}
void merge_sort(int arr[], int sx, int dx)
{
if (sx < dx){
int m = (sx+dx)/2;
merge_sort(arr, sx, m);
merge_sort(arr, m+1, dx);
unisci(arr, sx, m, dx);
}
}
Quick Sort
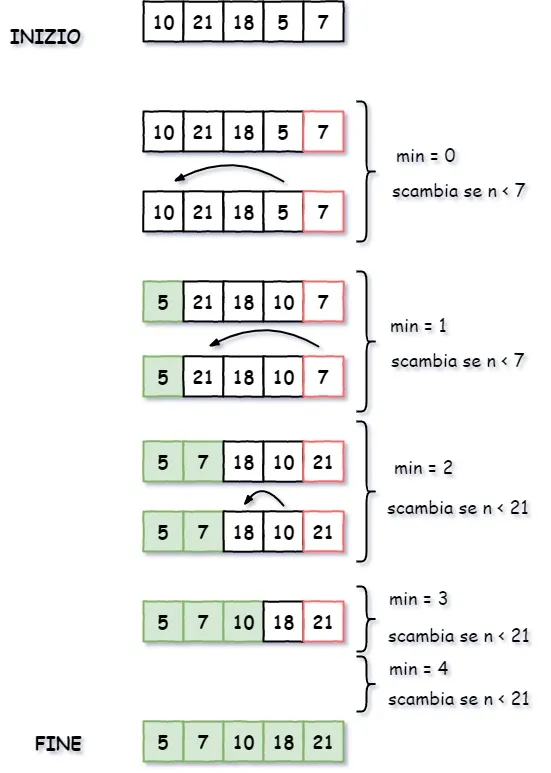
Il quick sort, assieme al merge sort è un algoritmo molto performante. L’array viene ordinato spostando gli elementi in base ad un valore di riferimento. Per fare questo si utilizza la ricorsione.
Partendo dall’inizio dell’array (con min = 0 e max = lunghezza dell’array) :
- Seleziona un punto di partizione dell’array tra min e max
- Sposta il punto di partizione nella posizione corretta, in base a quanti elementi sono più grandi e quanti più piccoli
- Sposta gli elementi più piccoli del punto di partizione da una parte, quelli più grandi dall’altra
- Richiama il punto 1 per l’array compreso tra min e il punto di partizione
- Richiama il punto 1 per l’array compreso tra il punto di partizione e max.
Pro
- Prestazioni elevate, complessità (O n log n)
- Gia implementato in c nella funzione qsort
int partiziona (int arr[], int min, int max){
int med = arr[max];
int i = (min - 1);
int j;
int tmp;
for (j = min; j <= max - 1; j++){
if (arr[j] < med){
i++;
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
tmp = arr[i + 1];
arr[i + 1] = arr[max];
arr[max] = tmp;
return (i + 1);
}
void quick_sort(int arr[], int min, int max){
if (min < max){
int part = partiziona(arr, min, max);
quick_sort(arr, min, part - 1);
quick_sort(arr, part + 1, max);
}
}
Quick sort è già stato implementato in C con la funzione qsort, per usarla è necessario definire una funzione comparatrice e passarla a qsort assieme all’array da ordinare, la lunghezza e il tipo di elemento.
qsort si trova in stdlib.h.
#include <stdio.h>
#include <stdlib.h>
int compara (int * a, int* b)
{
return *a - *b;
}
int main ()
{
int i;
int arr[] = { 12,312,62,345,23,1 };
qsort (arr, 6, sizeof(int), compara);
for (i=0; i<6; i++){
printf ("%d ",arr[i]);
}
return 0;
}
Introdurre una funzione di comparazione risulta molto utile quando dobbiamo ordinare tipi complessi o effettuare più ordinamenti secondo criteri diversi.
typedef struct info{
int codice;
char nome[50];
char cognome[50];
}persona;
int ordina_per_codice (info* a, info* b)
{
return *a->codice - *b->codice;
}
int ordina_per_nome (info* a, info* b)
{
return strcmp(*a->nome, *b->nome);
}
int ordina_per_cognome (info* a, info* b)
{
return strcmp(*a->cognome, *b->cognome);
}
